What Is the Ph of a Solution of 1.4x10 3
Acids and Bases
There are several definitions of what constitutes an acid:
The Arrhenius definition: By the 1884 definition of Svante Arrhenius (Sweden), an acid is a material that can release a proton or hydrogen ion (H+).
The Lewis definition: A Lewis acid is one that can accept a pair of electrons and form a coordinate covalent bond.
The Brønsted-Lowry definition: Brønsted argued that all acid-base reactions involve the transfer of an H+ ion, or proton. Water reacts with itself, for example, by transferring an H+ ion from one molecule to another to form an H3O+ ion and an OH- ion. According to this theory, an acid is a "proton donor" and a base is a "proton acceptor."
For now we will stick with the Brønsted-Lowry definition. And we will now tie the concept of acids and bases into equilibrium:
Let's start by looking at the Ionization of Water:
2H2O(l) <=> H3O+(aq) + OH-(aq)
This reaction does fit the Brønsted-Lowry definition since one water molecule is acting as an acid "donating" a proton and the other is acting as a base "accepting" the proton:
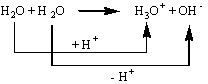
If we now write this reaction into an equilibrium expression:
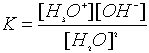
But remember one of our rules regarding the writing of equilibrium expressions states that we do not include solvents (liquids) as their concentration stays pretty constant during a reaction so the water portion of the equation is essentially equal to 1 and thus "disappears".
The resulting equation is given a special designation KW called the ionization constant of water: ![]()
The value of this constant at 25oC is 1.0 x 10-14. As you can see from the very small value of KW, water is not very dissociated at room temperature and our assumption that the concentration of water being constant is a good one.
For pure water, the values of [H3O+ ] and [OH- ] are equal and thus their values are both 1.0 x 10-7. If there is an equal amount of acid and base present in any solution, the solution is called "neutral" and the pH of the solution is 7.
If the acid concentration is greater than the base concentration, the solution is acidic and the pH will be less than 7. If the base concentration is greater than the acid concentration, the solution is basic and the pH will be greater than 7.
The pH Scale:
The pH of a solution is defined as the negative log10 [H+]
(NOTE: H+ and H3O+ are interchangeable ways to describe the presence of protons in solution)
The pOH of a solution is defined as the negative log10 [OH¯]
Conversely,
[H3O+] = 10-pH and [OH¯] = 10-pOH
The pH of a neutral solution is therefore 7. (-log[1 x 10-7] = 7)
The sum of the pH and pOH must always equal 14. This is because the –log KW = -log(1 x 10-14) = 14.
| Concentration (mol/L) | |||||
| [H 3 O + ] | pH | [OH - ] | pOH | ||
| 1 | 0 | 1 x 10-14 | 14 | | |
| 1 x 10-1 | 1 | 1 x 10-13 | 13 | ||
| 1 x 10-2 | 2 | 1 x 10-12 | 12 | ||
| 1 x 10-3 | 3 | 1 x 10-11 | 11 | Acidic Solution | |
| 1 x 10-4 | 4 | 1 x 10-10 | 10 | ||
| 1 x 10-5 | 5 | 1 x 10-9 | 9 | ||
| 1 x 10-6 | 6 | 1 x 10-8 | 8 | ||
| 1 x 10-7 | 7 | 1 x 10-7 | 7 | Neutral Solution | |
| 1 x 10-8 | 8 | 1 x 10-6 | 6 | | |
| 1 x 10-9 | 9 | 1 x 10-5 | 5 | ||
| 1 x 10-10 | 10 | 1 x 10-4 | 4 | ||
| 1 x 10-11 | 11 | 1 x 10-3 | 3 | Basic Solution | |
| 1 x 10-12 | 12 | 1 x 10-2 | 2 | ||
| 1 x 10-13 | 13 | 1 x 10-1 | 1 | ||
| 1 x 10-14 | 14 | 1 | 0 | ||
More generally, acid dissociation constants (Ka) are of the form:
Where [HA] is the reactant acid concentration, [H+] (also sometimes represented as [H3O+]) is the product acid concentration, and [A-] is the product base concentration.
The reactants and products in an acid-base equilibrium are called "conjugates" of one another. This is because the acid and base only vary by the addition or subtraction of a proton.
Example:
H3PO4 + H2O <=> H3O+ + H2PO4 -
In this case, the H3PO4 and H2PO4 - are acid and conjugate base respectively, and the H2O and H3O+ are base and conjugate acid respectively.
What are the conjugate bases of these acids?
| original acid | conjugate base |
| HNO3 | |
| H2O | |
| H3O+ | |
| H2SO4 | |
| HBr | |
| HCO3 - |
What are the conjugate acids of these bases?
| original base | conjugate acid |
| OH- | |
| H2O | |
| HCO3 - | |
| SO4 2- | |
| ClO4 - |
Answers
Strong Acids and Bases:
Now that we have defined what an acid is and how to define a solution as acidic or basic, let's talk about what makes an acid strong versus weak:
This again is an equilibrium concept. Strong acids are those that greatly dissociate in solution. There is a limited number of those acids, so you should be able to remember them (hint, hint).
HNO 3 - nitric acid
HCl - hydrochloric acid
H 2 SO 4 - sulfuric acid
HClO 4 - perchloric acid
HBr - hydrobromic acid
HI - hydroiodic acid
There are others that are not so common, but I wouldn't expect you to know those unless I gave you their Ka value. Generally, any acid with a pKa (-logKa) less than about -2 is said to be a strong acid.
Values of K a for Common Acids
| Strong Acids | K a | ||||
| hydrochloric acid | (HCl) | 1 x 106 | |||
| sulfuric acid | (H2SO4) | 1 x 103 | |||
| hydronium ion | (H3O+) | 55 | |||
| nitric acid | (HNO3) | 28 | |||
| Weak Acids | K a | ||||
| phosphoric acid | (H3PO4) | 7.1 x 10-3 | |||
| citric acid | (C6H7O8) | 7.5 x 10-4 | |||
| acetic acid | (CH3CO2H) | 1.8 x 10-5 | |||
| boric acid | (H3BO3) | 7.3 x 10-10 | |||
| water | (H2O) | 1.8 x 10-16 | |||
A strong base is able to deprotonate very weak acids in an acid-base reaction. Compounds with a pKa of more than about 13 are called strong bases. Common examples of strong bases are the hydroxides of alkali metals and alkaline earth metals like NaOH and Ca(OH)2.
A weak acid will have a strong conjugate base and a strong acid will have a weak conjugate base.
Example pH Calculations:
(1) What is the pH of (a) human blood, in which the hydronium ion concentration is 4.0 x 10-8 M; (b) 0.020 M HCl(aq); (c) 0.040 M KOH (aq); (d) household ammonia in which the [OH¯]= 3 x 10-3 M; (e) 6.0 x 10-5M HClO4(aq)
Answers: (a) pH = -log(4.0 x 10-8 M ) = 7.4; (b) pH = -log(0.020 M ) = 1.7; (c) pOH = -log(0.040) = 1.4 so pH = 14-1.4 = 12.6; (d) pOH = -log(3 x 10-3 M) = 2.5 so pH = 14-2.5 = 11.5; (e) pH = -log(6.0 x 10-5? M ) = 4.2
(2) Find the hydronium ion concentration in a solution with pH = 4.83
Answer: [H+] = 10-pH = 10-4.83 =1.5 x 10-5 M
(3)The pH of a solution of Ba(OH)2 10.66 at 25ºC. What is the hydroxide ion concentration in the solution? If the solution volume is 125 mL, how many grams of Ba(OH)2 must have been dissolved?
Answer:
14 – 10.66 = 3.34= pOH [OH-] = 10-pOH = 10-3.34 = 4.6 x 10-4 M
1 mole of Ba(OH)2 for every two moles of OH- so 4.6 x 10-4 mol OH x 1 Ba(OH)2/2 OH- = 2.3 x 10-4M Ba(OH)2
0.125 L x 2.3 x 10-4 M Ba(OH)2 = 2.9 x 10-5 moles Ba(OH)2 x 171g/mol = 4.9 x 10-3 g
What Is the Ph of a Solution of 1.4x10 3
Source: https://www.chem.fsu.edu/chemlab/chm1046course/acidbase.html